Hadron DaVinci

Posts on Code Challenges

• Update: Posting New Code Tutorials To Awesome Algorithms

  No longer will I be posting code tutorials to my blog, Instead, I’ll be posting them on
  Awesome Algorithms
  
  which is a non-profit organization I created that
  teaches complex code via animation.

• Heap Sort Tutorial

  Example

  Sort the given array with Heap Sort:

• Create Max Heap Tutorial

  Example

  Create a Max Heap with the following array. [-3, 11, 52, 4, 23, 70, 65, 100]

• Quick Sort Tutorial

  Example

  Sort the given array with Merge Sort:

  A = [5, 2, 4, 6, 1, 3]
  quick_sort(A)
  assert(A) == [1, 2, 3, 4, 5, 6]
  

  
  

• Merge Sort Tutorial

  Example

  Sort the given array with Merge Sort:

  A = [5, 2, 4, 6, 1, 3]
  merge_sort(A)
  assert(A) == [1, 2, 3, 4, 5, 6]
  

  
  

• Insertion Sort Tutorial

  Example

  Sort the given array with Insertion Sort:

  A = [5, 2, 4, 6, 1, 3]
  insertion_sort(A)
  assert(A) == [1, 2, 3, 4, 5, 6]
  

  
  

• Bubble Sort Tutorial

  Example

  Sort the given array with Bubble Sort:

  A = [5, 2, 4, 6, 1, 3]
  bubble_sort(A)
  assert(A) == [1, 2, 3, 4, 5, 6]
  

  
  

• Selection Sort Tutorial

  Example

  Sort the given array with Selection Sort:

  A = [5, 2, 4, 6, 1, 3]
  selection_sort(A)
  assert(A) == [1, 2, 3, 4, 5, 6]
  

  
  

• Complete A Sudoku Board

  

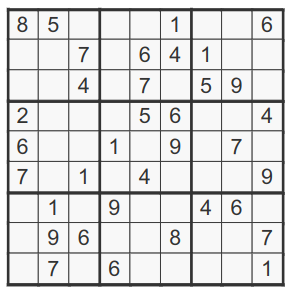
• Verify If A Sudoku Board Is Correct

  

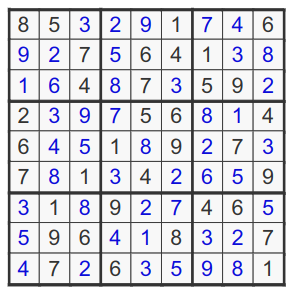
• Rotate Array 270 Degrees

  

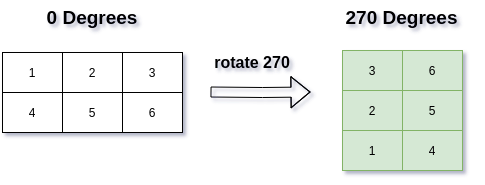
  Problem

  Given an array, rotate it 270 degrees.
  
  

• Find Contiguous Sub-Sequence

  For many programming challenges, it is often beneficial to find contiguous sub-sequences
  given a sequence. Note, the sequence may represent an array, a string, etc.

  Problem

  Given an array, find contiguous subarrays.
  
  

• Find Min and Max Sum From Subarray

  Problem

  Given an array, create an algorithm which determines the minimum and maximum sum that can be obtained from any subarrays.
  
  

• Kadanes Algorithm

  
  

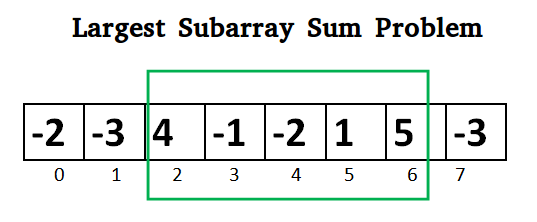
• Reverse Position of All Letters Except Symbols

  

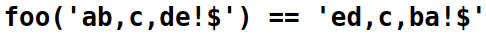
  Problem

  Given a string, reverse the position of every letter in that string except non-letters.
  
  

• Minimum Number From Increasing and Decreasing Digits

  Problem

  Given a string containing only I’s and D’s, where I’s represent an increase of 1 between adjacent digits
  and D’s represent a decrease of 1 between adjacent digits, create a function named foo which determines
  the minimum number formed by digits 1 through 9 that matches that pattern, given that no digits can repeat.
  
  

• Partial Permutations

  A partial permutation is known as a P(n,k) problem which means we must select permutations
  of size k out of n objects. There are numerous algorithms for calculating partial permutations
  but I wanted one that seemed more intuitive.
  

• Sum of Numbers in Binary Tree Paths

  

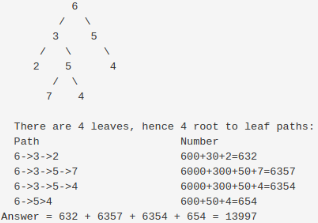  Problem
  Find the sum of all the numbers represented by a binary tree given that each node represents a digit in numbers formed by paths from root to leaf.

• Build Binary Tree from Postorder

  

  
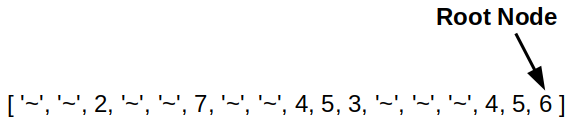
  Problem
  Build a binary tree from a list that represents the postordering of nodes. Where ~ represents a null node. Then print the preorder, inorder, and postorder of tree nodes as a list.

• Build Binary Tree from Preorder

  

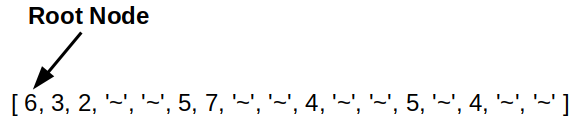  Problem
  Build a binary tree from a list that represents the preordering of nodes. Where ~ represents a null node. Then print the preorder, inorder, and postorder of tree nodes as a list.

• Count Number of Strings of Length N

  Problem

  Count the number of strings of length n=3,
  that can be made using a, b, and c with at most one b and two c’s allowed.
  
  

• Full Permutations

  Most code challenges are based on combinatorics so having an understanding of the fundamentals is
  essential. In this problem, we’ll calculate full permutations of a given array.

• Doing Full Permutations by Hand

  We will do full permutations by hand with the bottom up approach.
  Note, the difference between a full permutation and partial permutation is that in a full permutation,
  the number of items selected equals the number of items in the original set. The insights from this can be used to create code which does this automatically.

• Partial Combinations

  Most code challenges are based on combinatorics so having an understanding of the fundamentals is
  essential. A partial combination is known as a C(n,k) problem which means we must select combinations
  of size k out of n objects.
  
  In this problem, we’ll calculate combinations of a given array.

• Doing Partial Combinations by Hand

  We will do combinations by hand with the bottom up approach.
  The insights from this can be used to create code which does this automatically.

• Calculate the Absolute Difference of Diagonal Sums

  Problem

  Given a square matrix, calculate the absolute difference between the sums of its diagonals.
  

• Minimum and maximum number of coins needed to make change for a $100 dollar bill? (Unbounded)

  Problem

  You have unlimited $20 dollar bills, unlimited $10 dollar bills, unlimited $5 dollar bills, and unlimited $1 dollar bills.
  How many ways can you make change for a $100 dollar bill?
  
  

• Minimum and maximum number of coins needed to make change for a $100 dollar bill? (Bounded)

  Problem

  You have three $20 dollar bills, five $10 dollar bills, two $5 dollar bills, and five $1 dollar bills.
  How many ways can you make change for a $100 dollar bill?
  
  

• Ways can you make change for a $100 dollar bill? (Bounded)

  Problem

  You have three $20 dollar bills, five $10 dollar bills, two $5 dollar bills, and five $1 dollar bills.
  How many ways can you make change for a $100 dollar bill?
  
  

• Coin Change Problem Mother Function

• Find Value at Middle Node in Double Linked List

  Problem

  Find Middle Node of Double Linked List:
  1 <=> 2 <=> 3 <=> 4 <=> 5 <=> 6
  
  

• Find Value at Middle Node in Single Linked List

  Problem

  Find Middle Node of Single Linked List:
  1 => 2 => 3 => 4 => 5 => 6