Complete A Sudoku Board
06 Feb 2021 - Hadron DaVinci
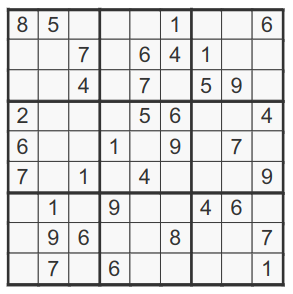
Problem
Given a 9x9 array which represents a Sudoku board, select the missing elements, represented by 0’s
such that the array meets the Sudoku criteria.
A Sudoku board is valid when three criterion are met:
- Each row contains unique values from 1-9.
- Each column contains unique values from 1-9.
- Each of the 9 sub-squares, of size 3x3, contains a unique value from 1-9.
Example
Given
A = [
[8, 5, 0, 0, 0, 1, 0, 0, 6],
[0, 0, 7, 0, 6, 4, 1, 0, 0],
[0, 0, 4, 0, 7, 0, 5, 9, 0],
[2, 0, 0, 0, 5, 6, 0, 0, 4],
[6, 0, 0, 1, 0, 9, 0, 7, 0],
[7, 0, 1, 0, 4, 0, 0, 0, 9],
[0, 1, 0, 9, 0, 0, 4, 6, 0],
[0, 9, 6, 0, 0, 8, 0, 0, 7],
[0, 7, 0, 6, 0, 0, 0, 0, 1],
]
Then:
solve_sudoku(A) = [
[8, 5, 3, 2, 9, 1, 7, 4, 6],
[9, 2, 7, 5, 6, 4, 1, 3, 8],
[1, 6, 4, 8, 7, 3, 5, 9, 2],
[2, 3, 9, 7, 5, 6, 8, 1, 4],
[6, 4, 5, 1, 8, 9, 2, 7, 3],
[7, 8, 1, 3, 4, 2, 6, 5, 9],
[3, 1, 8, 9, 2, 7, 4, 6, 5],
[5, 9, 6, 4, 1, 8, 3, 2, 7],
[4, 7, 2, 6, 3, 5, 9, 8, 1],
]
Observations:
These are the following limitations for each empty element in Sudoku board.
- Each row contains unique values from 1-9.
- Each column contains unique values from 1-9.
- Each of the 9 sub-squares, of size 3x3, contains a unique value from 1-9.
Method 1
-
For each empty element, find a set of possible numbers based on limitations imposed by that element’s row, column, and sub-square.
-
Try each possible number and use recursion to see if it’s possible to solve resulting Sudoku Board
-
If a possible number does not result in a solution, then back track and try the next number
Method 1 Complexity
Given NxN matrix, and N=9
TC: 9^(NxN)
SC: NxN
Method 1 Solution
Method 2
Same a Method 1 but the iterator that selects empty
elements is implemented differently.
Method 2 Complexity
Given NxN matrix, and N=9
TC: 9^(NxN)
SC: NxN
Method 2 Solution