Hadron DaVinci

Kadanes Algorithm

25 Dec 2020 - Hadron DaVinci

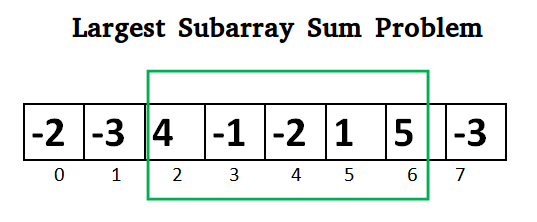
Kadane’s algorithm can be used to find the max sum in any contiguous subarray.

Examples

kadane([-2, -3, 4, -1, -2, 1, 5, -3]) == 7

kadane([2, -1, -2, 1, -4, 2, 8]) == 10

kadane([-1, -1, -1]) == -1

---

Methods

Method 1

Time Complexity: O(N)
Spatial Complexity: O(1)

Method 1 Summary
The idea here is to loop through each number in the array and keep track of a running total.
Once the running total becomes negative, since we’re trying to find the maximum,
(it is not advantageous to hold on to that negative value), reset the running total as the current number.

1. Initialize variables
   • set best_sum at negative Infinity.
     • We do this b/c we’re going to maximize best_sum
   • set running_total at Zero
     
     
2. Loop through each number:
   • When running_total is negative:
     • set running_total to Zero.
       this represents the start of a new sub array sum
   • add this_number to running_total
   • Set best_max as the maximum of (best_max and the current running_total)
     • if best_max actually does get updated,
       that represents the end of a subarray
       
       
3. Return best_max

Method 1 Solution

def kadane(arr: list) -> int:
    best_sum = float('-inf')
    running_total = 0

    for this_number in arr:
        if running_total < 0:
            running_total = 0

        running_total += this_number

        best_sum = max(best_sum, running_total)
    return best_sum

# Try Code
if __name__ == "__main__":
    assert kadane([-2, -3, 4, -1, -2, 1, 5, -3]) == 7
    assert kadane([2, -1, -2, 1, -4, 2, 8]) == 10
    assert kadane([-1, -1, -1]) == -1

---

Method 2

Time Complexity: O(N)
Spatial Complexity: O(1)

Method 2 Summary
This method is really the same as method1. The only difference is that logic
for setting running_total has been consolidated to one line.

Personally, I prefer method1 since method2 obscures some of the logic
being used.

1. Initialize variables
   • set best_sum at negative Infinity.
     • We do this b/c we’re going to maximize best_sum
   • set running_total at Zero
     
     
2. Loop through each number:
   • Set running_total as the maximum of (this_number and (running_total + this_number))
     • This is a shorthand way of saying:
       If running_total is less than 0, then set running_total equal to this_number
   • Set best_max as the maximum of (best_max and the current running_total)
     
     
3. Return best_max

Method 2 Solution

def kadane(arr: list) -> int:
    best_sum = float('-inf')
    running_total = 0

    for this_number in arr:
        running_total = max(this_number, running_total + this_number)
        best_sum = max(best_sum, running_total)
    return best_sum

# Try Code
if __name__ == "__main__":
    assert kadane([-2, -3, 4, -1, -2, 1, 5, -3]) == 7
    assert kadane([2, -1, -2, 1, -4, 2, 8]) == 10
    assert kadane([-1, -1, -1]) == -1

---

Files

method1.py
method2.py